Summary:
Learn how Lean Six Sigma helped ensure sustainable process improvement by aligning emergency department staffing with patient-arrival demand without increasing resource hours.
Learn how Lean Six Sigma methodology helped ensure sustainable process improvement by aligning ED staffing with patient-arrival demand — without increasing resource hours.
ABSTRACT: Thanks to the application of a well-defined Lean Six Sigma methodology to ensure sustainable process improvement, a queuing model at Lehigh Valley Health Network aligned emergency department staffing with patient-arrival demand — without increasing overall resource hours. It trimmed length of stay by as much as 20 percent and reduced walkouts by 58 percent, and the success is being replicated broadly across the network’s emergency departments.
***
BUILD A QUEUING MODEL
To forecast the impact of process variations on queues and patient wait time, the following three correlations can effectively construct a queuing model.
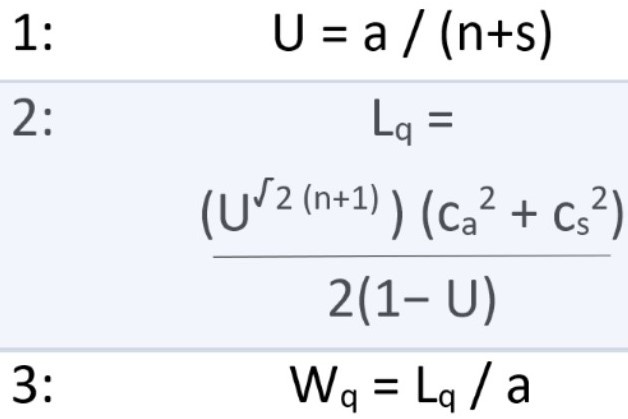
U - Use of servers (0 to 100 percent)
a - Average arrival rate (number of patients per hour)
n - Number of servers
s - Average server rate per server (number of patients per hour per server)
Lq - Number of patients waiting in the queue
ca - Coefficient of variation of arrival (standard deviation/mean)
cs - Coefficient of variation of server (standard deviation/mean)
Wq - Patient wait time
The health care industry worldwide is plagued with delays. We are used to waiting for an appointment to see a physician or schedule a procedure, and when we arrive at the physician’s office, we wait again to be seen. In hospitals, we often find patients waiting for beds in hallways, and delays for surgery or diagnostic tests are common.
There are numerous consequences to waiting — delayed care, poor patient satisfaction, financial implications and more. Today, more than ever, the application of queuing theory is a call to action for optimizing patient flow across our complex industry .
Queuing theory deals with delays caused by the disparity between demand for a service and the capacity to meet the demand. The purpose of a queuing model is to balance customer service (shorter wait time) and resource limitation (number of servers).
Queuing theory is used extensively in different industries, including banking, shipping and transportation. In health care, queuing models can be applied effectively to manage the flow of unscheduled patient arrivals in different areas, including the emergency department, operating rooms, intensive care units and diagnostic labs.
Queuing models can help forecast answers to questions about patient flow, such as:
How long will the average patient have to wait?
How long will it take for an average visit?
What is the likelihood a patient will have to wait for more than 20 minutes?
How long are providers occupied with an average patient?
How many staffers are necessary for all patients to be seen within 10 minutes?
Will patient flow improve if the triage process is different?
How likely is a hospital to divert patients to another hospital?
In health care, queuing models are generally based on three factors and the variation within.1 Those factors are patient arrival rate, server rate (service time for exam, treatment, etc.) and the number of servers (clinical and nonclinical staff) available.
In the emergency department, the arrival rate (“a must be less than unity (i.e., a times s equals less than 1). This is also known as server use rate (“U”). In the absence of variability, as long we can hold U”) is the unscheduled arrival frequency of patients that follows the Poisson distribution,2 indicating a high degree of variability within short intervals. Server rate (“ to less than 1, no queue will build up and the flow through the station would be regular.3 In the real world of variability, which very much exists in health care, queues are going to build. The closer U is to 1 (i.e., 100-percent use rate), the longer the queue for that station.s”) is the average time spent serving a particular type of patient at a given process step or station. In health care, unlike most manufacturing operations, the server rate is often random and is commonly described by an exponential probability distribution. The number of servers (“n”) is the number of staff or stations doing similar tasks for all patients who approach those stations. For a station with a single server, average arrival rate of patients (a) multiplied by the server rate (s)
For a complex ED operational process, relying solely on averages can mask process variability and lead to inaccurate forecasts. It is necessary to incorporate process variability and trends into correlations and approximations that are proven and tested in other industry applications. There are three key parameters to a queuing model: server use (U); queuing length, or number of patients waiting in line (“Lq”); and patient wait time (“Wq”).4 These three variable parameters are interrelated and can be described as follows:
Server use (U) is directly proportional to the arrival rate and inversely proportional to the server rate.
Queuing length (Lq) can change rapidly based on server use. It also is highly sensitive to variation in arrival rates and variation in server rates.
Patient wait time (Wq) is directly proportional to queuing length and inversely proportional to arrival rate.
These three parameters are the basis for the queuing model for an emergency department operation (see box above: Build a Queuing Model). The correlations are tested and proven by a variety of emergency departments across the nation.4
A Simple Queuing Model
Our organization, Lehigh Valley Health Network, used the correlations in the box to develop its queuing models. Required patient arrival data was obtained from the network’s electronic medical records system.
The first correlation estimates the average server use (U) based on staffing plan and average arrival rates (number of patients per hour) for each hour of the day. Figure 1 shows the average arrival rate for a specific ED in the network, which serves an average of 25,000 patients a year. As indicated earlier, patient arrival rate follows a Poisson distribution; frequency of arrival is random and the number of patients arriving at a certain hour can vary significantly from day to day. For example, this ED has an average patient arrival rate of five patients an hour during its 11 a.m. peak hour. However, on certain days, the arrival rate can be as high as 10 patients an hour during the same peak hour.
The second correlation estimates the number of patients in the queue (Lq) and (cs) have an exponential relationship with (Lq). Reducing operational variations can therefore significantly reduce the number of patients in queue (Lq) and the corresponding wait time (Wq).), which is a function of server use (U), coefficient of variation of arrival rate (ca) and coefficient of variation of server rate (cs). The correlation of variation is expressed as a ratio of the standard deviation (sigma) divided by mean. Note that both coefficients (ca
The third correlation, based on Little’s Law, can be used to estimate average wait time (Wq) for the patients at different hours of the day.
Tables 1 and 2 compare the “before” and “after” staffing plan for this emergency department. Table 1 shows the reactive nature of a traditional staffing plan where staff use (U) exceeds 100 percent during the early peak hours (7 a.m. to 2 p.m.).
Based on EMR data and observation testing at this emergency department, provider server rate is measured at 1.7 patients an hour and registered nurse server rate is 0.80 patients an hour. Table 1 shows the output of the “before” staffing plan, suggesting inadequate provider and RN staffing levels between 7 a.m. and 2 p.m. Once staff use (U) approaches 100 percent, queue length (Lq) and patient wait time (Wq) increase rapidly. Periods of understaffing and overstaffing specific to provider resources are illustrated in Figure 2 .
The data in Table 1 suggest the ED is understaffed during peak hours and overstaffed during off-peak hours. Traditional staffing plans for RNs also follow a similar trend. This is common for many EDs, where the psychology of staffing tends to be reactive. Staffing capacity is increased only after the pain is realized, generally at the onset of peak hours.
In contrast, Table 2 shows a balanced resource plan where capacity is aligned with hourly demand. Resource use (U) is maintained well below 100 percent. In many instances, as in this case, higher throughput, stability and operational efficiency can be achieved by merely aligning capacity with demand without increasing overall ED staffing hours.
Figures 2 and 3 are graphical representation of the outcomes (queuing length and patient wait time) from Tables 1 and 2, respectively. Once the queuing model is developed for a specific operational process, such as the emergency department here, different staffing plans can be entered into the model and evaluated before pilot testing.
Figure 2, corresponding to the “before” provider staffing plan of Table 1, shows alarmingly high wait times (more than 200 minutes) during early peak hours. Consequently, the number of patients in queue is shown as undefined per the model because provider use exceeds 100 percent. It is not surprising that patients leaving without being seen follows a similar trend. Most cases of LWBS occur during peak hours.
Figure 3 shows an improved staffing plan with adjustments to the shifts without altering overall ED resource hours. In this example, the 60 provider hours over a 24-hour period remained constant. Per the model, number of patients in queue is much improved and maintained below three and maximum wait time is around 30 minutes.
A queuing model is not limited to optimizing staffing. It can identify productivity gaps and variations in the process that leads to lower operational efficiency. Once a model is constructed, a series of sensitivity analyses can be performed, including staff productivity impact, staff productivity variations, impact of fast-track line, impact of providers in triage, and other parameters.
Results Achieved
Implementing the model was achieved by a multidisciplinary team, including representatives that ranged from frontline clinicians to hospital leadership.5 One challenge with implementing queuing theory is overcoming the perception that it involves advanced knowledge of math and statistics.6,7 On the contrary, proven and tested queuing models, correlations and approximations are readily available that can be used to analyze various patient flow parameters.4
Commercially available simulation models have some advantages, but there is value in constructing a basic queuing model in a spreadsheet based on the three correlations. It will make the operation-specific input and output variables transparent to the project team and the client. It also will improve alignment and planning and foster a superior decision process. In addition, most health care systems today have the necessary technology (e.g., EMR systems) that can provide patient arrival-to-discharge data necessary to construct the queuing model.
Queuing theory correlations are tested, proven and published by several others.4,8,9 Qualitatively, reduction of queuing lengths and corresponding patient wait times were quite evident at the network’s EDs. The network, therefore, did not take the time to elaborate and scientifically validate the model’s outcome accuracy. Instead, the focus was predominantly on evaluating standard ED operational metrics — namely, leaving without being seen and length of stay, and components of overall LOS, including “door to room” and “door to provider.”
Figure 4 shows a significant improvement to the overall LOS at the emergency department based on a weeklong rapid-cycle testing. Average LOS reduced from 245 minutes to 197 minutes (20 percent reduction) by merely aligning the ED staffing plan. For the patient population (1,296), process variation, measured in standard deviation, improved from 199 minutes to 159 minutes (20 percent reduction). Other process metrics within the overall LOS, namely “door to room” and “door to provider,” improved by 12 percent and 29 percent, respectively. The primary change at this facility was the addition of a new provider shift, 10 a.m. to 10 p.m.
Overall ED provider hours were held constant by reducing provider staffing levels during off-peak hours. Figure 5 shows average LOS by hour, as well as the direct impact of the new provider shift. Hourly LOS improved noticeably from the start of the 10 a.m. peak hour through late evening.
ED metrics of door-to-provider and LWBS are strong indicators of patient satisfaction.10
Figure 6 shows a significant improvement to LWBS at another network emergency department. This particular ED was faced with front-end challenges that resulted in long door-to-provider durations. Consequently, it historically reported higher LWBS data as a result of dissatisfied patients waiting too long to see a provider. Introducing a provider-in-triage process flow at the front end enabled segmentation of patient flow, in which lower-acuity (Emergency Severity Index 4 and 5) patients would go through the provider-in-triage, and higher-acuity patients (ESI 1,2,3) would continue to follow the main ED path.
This segmentation improved overall LOS for lower-acuity patients by 35 percent. The door-to-room and door-to-provider process metrics also improved by 36 percent and 43 percent, respectively. Such dramatic improvement also was attributed to being able to keep lower-acuity patients vertical; most of them were processed directly from triage to discharge without a bed assignment. LWBS for this facility improved by 58 percent. Standard deviation of daily LWBS percentage for the patient population (229) improved from 6.4 percent to 3.1 percent — a 52 percent reduction.
Future Application
Queuing theory is an integral part of Lean Six Sigma improvement methodology at Lehigh Valley Health Network, a critical tool during the planning phase that provides a sound framework for process optimization that includes staffing plan productivity. Given the recent success with its application at network ED locations, Lehigh Valley is planning to replicate similar improvements broadly across the network.11,12 Inpatient flow is a natural extension to the emergency department. Work is already underway at the inpatient unit to unveil defects and variations associated with admission-to-discharge processes.
Queuing models also can optimize discrete processes, such as physician practice office flow. Lehigh Valley’s physician practice groups, which include more than 170 practices (primary care and specialties), tend to have unique patient flow characteristics. Each practice can be modeled and optimized, resulting in less-crowded waiting rooms and faster appointments.
A final note: Queuing model is only a theoretical model that statistically can predict the future operational state based on implementing certain physical, behavioral and work process changes. The model provides only direction and confidence to the improvement team; the team members still must do the heavy lifting of implementation and associated change management. Application of queuing model in isolation, without a strong implementation team, does not guarantee project success. Nevertheless, queuing theory promotes team alignment, team focus and will continue to drive us toward our patient experience goal: approaching zero wait time for our patients.
Naser M. Chowdhury , PE, LSSBB, is director of the project management office for Lehigh Valley Health Network, in Allentown, Pennsylvania.
Lawrence Riddles, MD, MBA, FACS, FACPE, is regional chief medical officer for Lehigh Valley Health Network, in Allentown, Pennsylvania.
Richard Mackenzie, MD, MBOE, LSBB, FACEP, is senior vice chairman in the Emergency and Hospital Medicine Department for Lehigh Valley Health Network, in Allentown, Pennsylvania.
ACKNOWLEDGEMENTS: The authors thank Jessica Spack (project manager), Chris Kita (senior Lean coach), Lori Lawson (ED physician lead), Susan Curry (vice president, patient care services), Gary Bonfante (ED physician lead), Michaele Roberts (vice president, patient care services) and other members of the project teams. This work would not be possible without the support of leadership, including William Reppy (president), John Fletcher (president) and David Burmeister (chair, emergency medicine).
REFERENCES
Palvannan RK and Teow KL. Queueing for healthcare, Journal of Medical Systems, 2012, 36(2):541-547.
Huang, XM. A planning model for requirement of emergency beds. IMA Journal of Mathematics Applied in Medicine and Biology, 1995, 12(3-4): 345-352.
Takagi H, Kanai Y and Misue K. Queueing network model for obstetric patient flow in a hospital, Health Care Management Science, 2016, 03:03.
Gombolay M, Golen T, Shah N. and Shah J. Queueing theoretic analysis of labor and delivery: Understanding management styles and C-section rates, Health Care Management Science, 2017, 04:04.
Building a Better Delivery System, National Academy of Engineers and Institute of Medicine, Modeling and Simulation, The National Academy Press, Washington, D.C., 2005, 36, 37.
Crane J and Noon C. The Definitive Guide to Emergency Department Operational Improvement, CRC Press, 2011, 122, (119-145), (309-325).
Anonymous. ED revamp: team approach to care reduces errors, boosts patient and clinician satisfaction, ED Management, 2011, 23(7):78-80.
Foster EM, Hosking MR and Ziya S. A spoonful of math helps the medicine go down: an illustration of how healthcare can benefit from mathematical modeling and analysis, BMC Medical Research Methodology, 2010, 10:60.
Wiler JL, Bolandifar E, Griffey RT, Poirier RF and Olsen T. An emergency department patient flow model based on queueing theory principles, Academic Emergency Medicine, 2013, 20(9):939-946.
Lantz B and Rosen P. Measuring effective capacity in an emergency department, Journal of Health Organization & Management, 2016, 30(1):73-84.
Fitzgerald K, Pelletier L and Reznek MA. A Queue-Based Monte Carlo Analysis to Support Decision Making for Implementation of an Emergency Department Fast Track, Journal of Healthcare Engineering, 2017, 2017:6536523.
Patel PB and Vinson DR. Team assignment system: expediting emergency department care, Annals of Emergency Medicine, 2005, 46(6):499-506.
Topics
Systems Awareness
Critical Appraisal Skills
Action Orientation
Related
How to Approach Business Ethics as Global Consensus Breaks DownThe Pandemic Proved That Remote Leadership WorksAmid Plummeting Diversity at Medical Schools, a Warning of DEI Crackdown’s ‘Chilling Effect’Recommended Reading
Strategy and Innovation
How to Approach Business Ethics as Global Consensus Breaks Down
Strategy and Innovation
The Pandemic Proved That Remote Leadership Works
Strategy and Innovation
Amid Plummeting Diversity at Medical Schools, a Warning of DEI Crackdown’s ‘Chilling Effect’
Problem Solving
Seven Tricky Work Situations, and How to Respond to Them
Problem Solving
The Importance of Mentorship
Problem Solving
How to Encourage the Right Kind of Conflict on Your Team
